Monty Hall Problem Simulator

The Monty Hall problem is one of the most famous mathematical problems in the scope of Probability Theory:

In a television game show the host asks a player to pick one out of three closed doors that are in front of the player. Behind two of the doors are goats and behind one door is a car that the player can win when he picks that door. After the player has selected one door (which remains closed), the host opens another door which has a goat behind it. The host then asks the player whether he wants to stay at the door he selected in the beginning or whether he wants to switch to the other closed door.

The question obviously is: Should the player switch the door or stay at the selected door?

Many people might say that it doesn't matter whether the player switches the door or not, because the probability to win the car is 50/50 anyways. Even though this seems reasonable because there are two identical closed doors, it is the wrong answer.

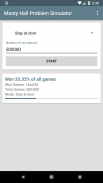
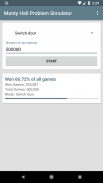
The correct answer is that the chance to win the car is 67% when the player switches the door and only 33% when the player stays at the door he selected first.

Don't believe met yet? Just download the app and try it out!

This app allows you to automatically simulate the described game scenario up to 5 Million times in a row. You can choose whether you want the simulated player to always switch the door or to always stay at the door he selected first. After the app has simulated the requested number of games, it gives you a statistic that shows you how many of the games the player has won. This way you can tell whether the player should or shouldn't switch the door.